九九を理解する覚え方教えます！暗記の苦手な大人も子供ももう安心◎

こんにちは、くみこママです(*^^*)

この記事では、九九を一生忘れない為に理解を伴う覚え方をご紹介します！
お子さんにテスト勉強ではなく、理解をさせたいお父さんお母さんへ。
そして、ご自身の見直し学習の為に。

早生まれな私の過去はとにかく暗記だった

１にも２にも、暗記。
ゆとり教育ではない義務教育時代で育った私は、これといって分析＋理解などをする間もなく、暗記(＠_＠)
自分でいっちゃなんですが、すさまじい記憶力の持ち主だったかもしれません。
ほぼ暗記だけで、中学、高校、大学へと進学したような覚えが。←
やばい人がここに。

早生まれな私は、小さい頃からクラスメイトはお兄さんお姉さんだらけという印象で、背伸びをしないとついていけない勝ち気さだけで、どうにかこうにか学生時代を過ごし抜いたような。
でも振り返ると、やってきた事って・・・ただのテスト勉強じゃない？

ある歳になってから気付いたことなのでした。
薄々わかっていたけど、←
人生に全く役立たないから意味がないのよね(ー_ー)と。笑
昔の自分がアホすぎて、情けない。

暗記は使わなければ、忘れます。

今更ですが、あらゆる事には理由があって理解できる事だと今の私は知っています。
記憶力だけに頼らず、ゆっくりであっても、全て理解しながら勉強されていくと生きた学習になると信じています。

呪文のような丸暗記は、大、大、大嫌いだ！

丸暗記してたやつが丸暗記を嫌いだす、現在３４歳女←

最近では、お勉強系の幼稚園からでも歌やリズムに合わせた九九の暗記活動を開始しています。
でもね、この丸暗記教育こそが苦手意識を持ってしまう所以なんだよ～！と私は教育者達に伝えたい。

先生の気持ちはわかります。
２桁の掛け算や割り算になれば、九九なしでは効率的に解くことができません。
そして、連立方程式などの応用的な段階へ進む為にも、九九は基礎の基礎です。
ただでさえますます難しくなるのに、いちいち考えなくても済むように、叩き込みたいんです。
確かに、丸暗記すれば計算力が格段に早くなるのです。

でも子供達からすれば、記憶だけでなく理解も一緒にしていきたいですよね。

そして、暗記の道一筋でやってきた私が言うとすれば、暗記は繰り返した回数で決まります。
小学校では、１の段から覚え、９の段の数字の順番に教育され、小さな段は繰り返し「唱える」回数が自然と多くなるので、５の段までは問題なく体に染みついているはずです。

ですが、九九の終盤に差し掛かると、どうでしょうか？

記憶が怪しいと感じる大人がどれだけ多いことか・・・！(@_@)
明らかに終盤ははしょり気味に、絶対的に少ない回数で覚えたはずです。
意外と終盤が大事だというのにね。笑

テレビのバラエティ番組でおバカタレントが九九の終盤を質問をされて、わけわかめな答えが返ってくる。
ちょっと情けなくなるけどヤバすぎて笑える。
まさにそんな状況ですね。

９の段っておもしろいよー！

学校が１から教えるなら、私は敢えて、９の段からいきます！笑

９の段は数の不思議に出会える瞬間です。

かける数が１増えると、１０の位が１上がり、１の位が１下がるのです。
また、かける数と１の位を足すと１０になるという発見も。

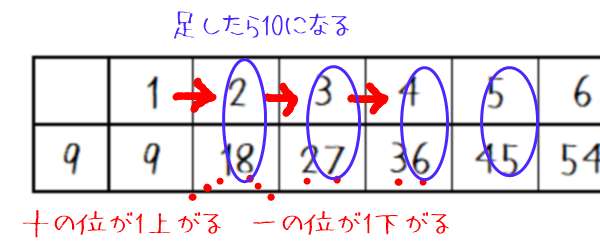
おおおっ！！

面白いってステキ！笑

くいちがく、くにじゅうはち、くさんにじゅうしち・・・

ね、呪文で覚える必要ある？

という話しです。

元の数ずつ増えている仕組みの理解

ぺらぺら出てくる呪文の暗唱もできるに越した事はありませんが、ただの暗記ではだめです。
そもそも足し算ができれば、掛け算の仕組みが理解できるはずです。

逆に言えば、暗唱を忘れてしまっても、足し算ができればOK！
だから、小学１年生でも理解できそうでしょ？

元の数が２であれば、

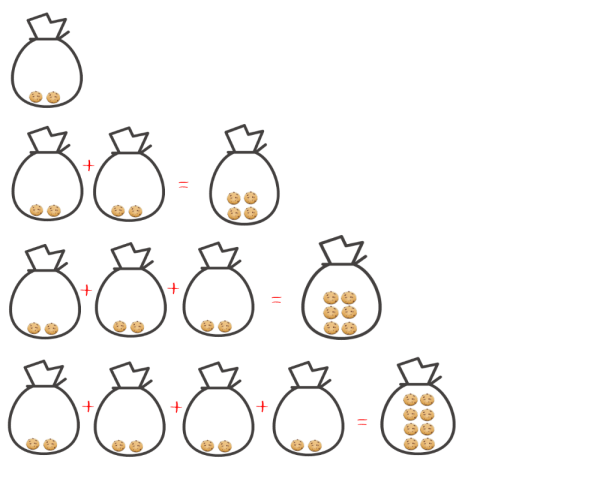
２ずつ増えていく事が理解できます。
元の数が３であっても７であっても、元の数ずつ増えるのです。

５なんて時計の針のイメージだよね～！笑
5  10 15 20 25 30 35 40 45。

なので、たとえ７×５＝３５がわかっていて７×６を忘れたとしても、３５＋７＝４２と導き出せます。

大きい数字であれば分解しても楽しいです。

上の例題と同じく、７×６＝○を求めるとします。

７を３と４に分解してみたとして、
(３×６)＋(４×６)＝１８＋２４＝４２

７を６と１に分解してみても、
(６×６)＋(１×６)＝３６＋６＝４２

仕組みさえ理解できていれば、算数は基本、答えさえ合っていれば、どんな方法で導きだしてもOKなわけです。
うっかりあれ？！となってもスラスラ出てくるはずですね。
ちなみに、わかりやすい掛け算の仕方として、指計算を推奨されている方もいます。
私は指よりイメージ派です。

リズミカルな暗唱も良いですが、自分なりにイメージして理解する力を一緒に学ぶ事で、面白さと自信に繋がる事を願っています。